Pounding out atomic nuclei
Nuclear reactions, from fission in reactors to fusion in stars, depend on interactions between protons and neutrons that are building blocks of atomic nuclei.
Describing all of the nuclei and the reactions between them, however, demands powerful algorithms running on high-performance computers.
The Universal Nuclear Energy Density Functional (UNEDF) collaboration, which was created by the Department of Energy’s Scientific Discovery through Advanced Computing (SciDAC) program, focuses on developing such descriptions.
The UNEDF collaboration includes researchers from seven national laboratories – Ames, Argonne, Lawrence Berkeley, Lawrence Livermore, Los Alamos, Oak Ridge, and Pacific Northwest – and nine universities: Central Michigan, Iowa State, Michigan State, Ohio State, San Diego State, North Carolina at Chapel Hill, Tennessee-Knoxville, Texas A&M in Commerce and University of Washington. Recently, researchers in this collaboration made a significant advance through the use of density functional theory (DFT).
On Earth, only about 300 kinds of nuclei – specific combinations of protons and neutrons – exist. In accelerators and stars, the number of known nuclei grows to about 3,000, and it could eventually expand to around 6,000. Many of these tiny systems prove extremely difficult to study, largely because they live such short lives before decaying.
Consequently, researchers need ways to accurately simulate these elusive species. Other applications also require extremely precise simulations of interacting nuclei. For example, the National Nuclear Security Administration (NNSA) Stockpile Stewardship Program requires such simulations to assess the safety and functionality of the weapons in the U.S. nuclear stockpile.
Witold Nazarewicz, professor of physics at the University of Tennessee and co-director of UNEDF, describes the basic structure: “A nucleus resembles a droplet of liquid, where there’s a high density inside and a surface area where it drops, and there’s little outside.” Moreover, the quantum behavior of the protons and neutrons at that surface determines the energy of the nucleus and how it interacts with other nuclei. “We need to know how the nuclear energy is generated in a nucleus to use it.”
Talented teamwork
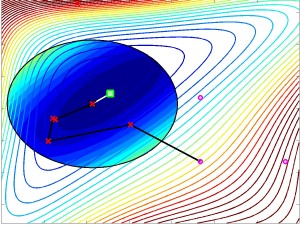
DFT provides an extremely useful, but not necessarily easy, approach to modeling nuclei. For one thing, DFT includes many parameters that must be determined. As Stefan Wild, assistant computational mathematician in the Laboratory for Advanced Numerical Simulations at Argonne and a fellow in the Computation Institute at the University of Chicago, asks, “What are the best parameters to calibrate these new models to experimental data?”
In the past, scientists searched for the best parameters with what Wild, an alumnus of DOE’s Computational Science Graduate Fellowship, calls “a lot of hand-tuning. They used intuition to pick the values of parameters, ran a simulation, saw how close the answer came to observed data, made small adjustments and ran the simulation again.”
Given the increasing complexity of nuclear simulations, however, “hand-tuning was like looking for a needle in a haystack and far too time consuming to do anything rigorous or thorough.”
As high-performance computing grew more powerful, though, Wild says that “people started thinking about doing something more mathematical” with DFT. For example, Wild and Jorge Moré, an Argonne Distinguished Fellow and director of Argonne’s Laboratory for Advanced Numerical Simulations, developed an algorithm and computer code called POUNDERS (for “practical optimization using no derivatives for sums of squares”).